Back in November I released colinodell/json5 - a JSON5 parser for PHP. It's essentially a drop-in replacement for PHP's json_decode() function, but it allows things like comments, trailing commas, and more.

Fast forward to this weekend when I received the following bug report from a user named Antonio:

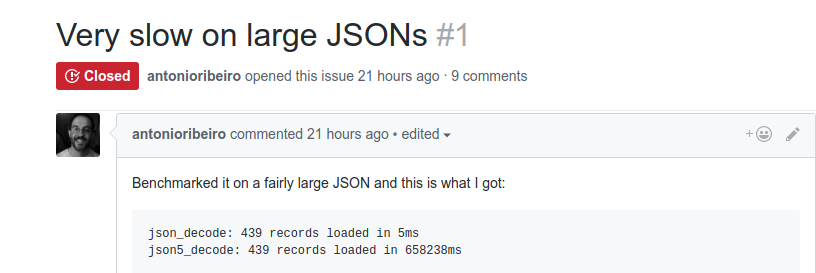
Yikes! I always knew that a PHP-based implementation would be slower than PHP's native C implementation, but execution time measured in minutes was completely unacceptable!

So I fired up Blackfire (which I've previously used to optimize league/commonmark) and got to work.

Getting a Baseline

The first step was to profile the current version to get a baseline. Instead of using Antonio's sample input (and needing to wait several minutes for a result), I decided to reduce that by one-tenth so I could profile, test, and iterate faster. Here's the results from that initial benchmark:

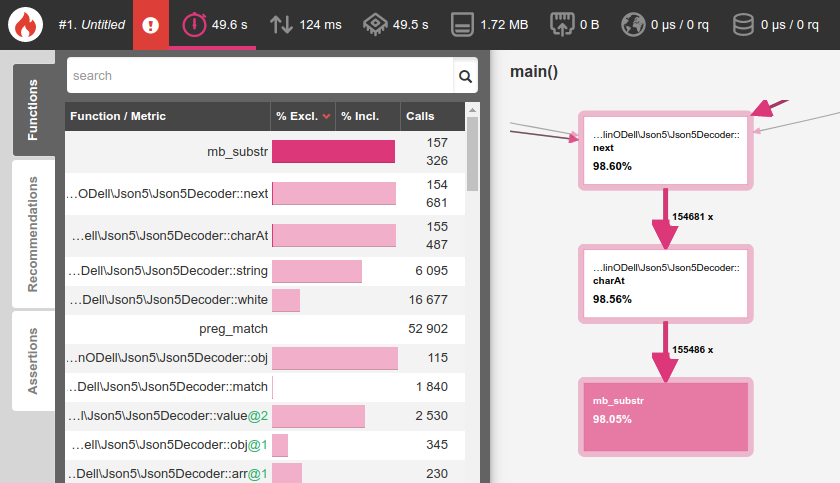
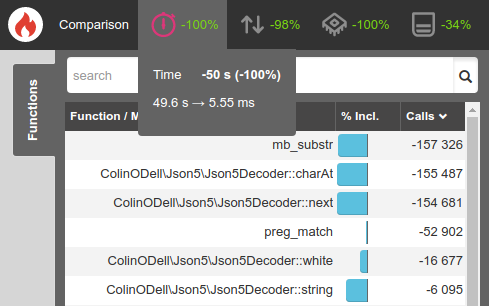
As you can see above, this sample JSON5 input took 49.6 seconds to execute! Let's see what we can do to optimize that.

Optimization 1

It was immediately clear that mb_substr() was the main culprit here - 98.05% of the execution time was spent calling this function. In fact, we were calling this function to fetch each individual character from the string (in order to know what character exists at the given position).

mb_substr() is a very expensive operation due to how UTF-8 strings work: encoded characters have variable lengths between 8 and 32 bits. If you want the 5th character you can't simply look at the fifth byte (like with ASCII strings) because you don't know how many bytes the preceeding 4 characters are using - you always need to count from the beginning of the string. So everytime my code wanted to know the character at position x it would use mb_substr() to read each individual character from the start of the string through position x.

Instead of performing this expensive operation multiple times, I borrowed a trick from league/commonmark to preg_split() a UTF-8 string into an array of multibyte characters:

$this->chArr = preg_split('//u', $json, null, PREG_SPLIT_NO_EMPTY);

I could now simply reference the index of the array to get the character I wanted:

     private function charAt($at)
     {
         if ($at < 0 || $at >= $this->length) {
             return null;
         }
 
-        return mb_substr($this->json, $at, 1, 'utf-8');
+        return $this->chArr[$at];
     }

(I also removed another minor usage of mb_substr() elsewhere in the code that wasn't necessary)

This change provided a massive performance improvement of 96%!

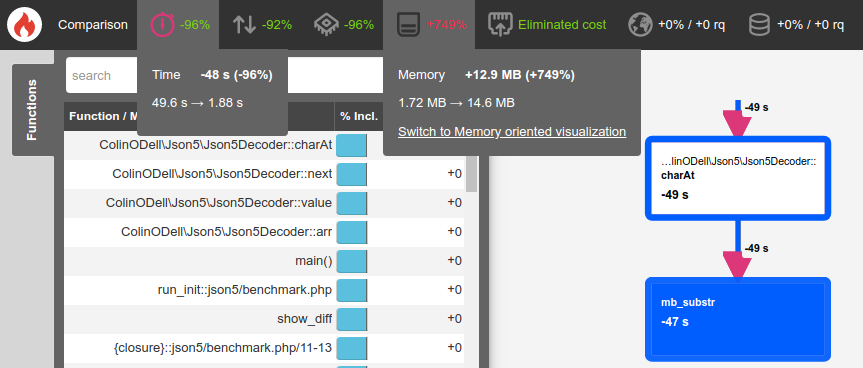
This 96% improvement was a major improvement (relatively speaking), but 1.88 seconds was still too long. Let's see what else we can do.

Optimization 2

The results from the previous profile showed that mb_substr() was still accounting for 65% of the execution time. This remaining usage was inside a regex helper function which attempts to match a regular expression at the given position:

private function match($regex)
{
    $subject = mb_substr($this->json, $this->at); // <--- Slow!
    $matches = [];
    if (!preg_match($regex, $subject, $matches, PREG_OFFSET_CAPTURE)) {
        return null;
    }

    // ...
}

This usage of mb_substr() was necessary because the offset feature provided by preg_match() works using bytes and not characters, which makes it useless for UTF-8. Because we can't use the offset parameter, we need to manually create a substring from the current position onwards and match against that.

The issue here was that mb_substr() was always starting at the beginning of the JSON input and spending time counting characters that we already parsed and no longer care about. I still need to perform the mb_substr() calls, but if I cache that "remainder" text (which gets smaller and smaller the more we parse) we can speed this up!

     private function match($regex)
     {
-        $subject = mb_substr($this->json, $this->at);
+        $subject = $this->getRemainder();
 
         $matches = [];
         if (!preg_match($regex, $subject, $matches, PREG_OFFSET_CAPTURE)) {
             return null;
         }

         // ...
     }
+
+    /**
+     * Returns everything from $this->at onwards.
+     *
+     * Utilizes a cache so we don't have to continuously parse through UTF-8
+     * data that was earlier in the string which we don't even care about.
+     *
+     * @return string
+     */
+    private function getRemainder()
+    {
+        if ($this->remainderCacheAt === $this->at) {
+            return $this->remainderCache;
+        }
+
+        $subject = mb_substr($this->remainderCache, $this->at - $this->remainderCacheAt);
+        $this->remainderCache = $subject;
+        $this->remainderCacheAt = $this->at;
+
+        return $subject;
+    }
 }

Not having to read through characters we don't care about resulted in a nice 32% boost, dropping execution time down to 1.27 seconds:

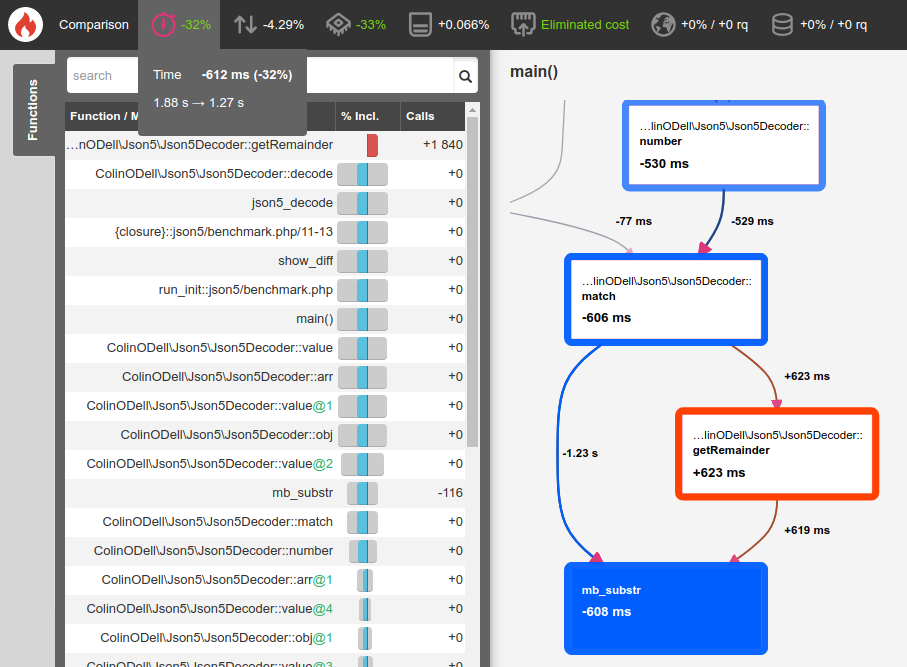
This doesn't eliminate the expensive mb_substr() call, but it does make it faster which is helpful.

Optimization 3

Even though we did a good job optimizing our match() function, it was still accounting for a large portion of the execution time. I therefore reviewed every usage of match() to see whether regular expression matching was necessary and if so how to optimize them.

I ended up finding three instances where regular expressions were always attempting a match a very specific character (or small set of characters) at the current position. For example, this one always requires an E or e at the current position:

if (($match = $this->match('/^[Ee][-+]?\d*/')) !== null) {

If we already know in advance what the first character is (hint: we do) then we check that first to avoid an expensive check which we know will fail! (You'll recall from the previous optimization that the regular expression itself isn't the expensive part, but rather the internal mb_substr() call that our match() function uses to get the string we're matching against.)

diff --git a/src/Json5Decoder.php b/src/Json5Decoder.php
index 46fec03..fa16400 100644
--- a/src/Json5Decoder.php
+++ b/src/Json5Decoder.php
@@ -262,10 +262,10 @@ private function number()
 
         switch ($base) {
             case 10:
-                if (($match = $this->match('/^\d*\.?\d*/')) !== null) {
+                if ((is_numeric($this->ch) || $this->ch === '.') && ($match = $this->match('/^\d*\.?\d*/')) !== null) {
                     $string .= $match;
                 }
-                if (($match = $this->match('/^[Ee][-+]?\d*/')) !== null) {
+                if (($this->ch === 'E' || $this->ch === 'e') && ($match = $this->match('/^[Ee][-+]?\d*/')) !== null) {
                     $string .= $match;
                 }
                 $number = $string;
@@ -309,7 +309,7 @@ private function string()
             }
 
             if ($this->ch === '\\') {
-                if ($unicodeEscaped = $this->match('/^(?:\\\\u[A-Fa-f0-9]{4})+/')) {
+                if ($this->peek() === 'u' && $unicodeEscaped = $this->match('/^(?:\\\\u[A-Fa-f0-9]{4})+/')) {
                     $string .= json_decode('"'.$unicodeEscaped.'"');
                     continue;
                 }

This shaved another 29% off and took execution down to 900ms!

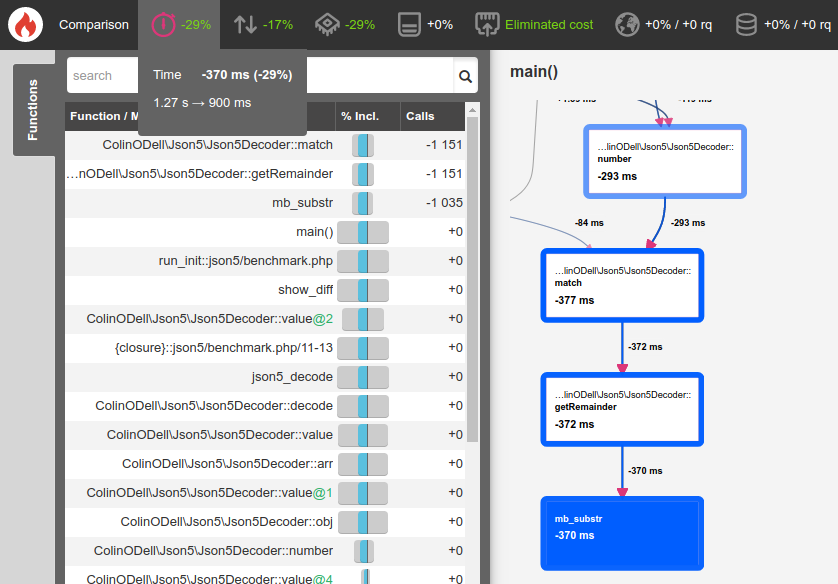
Micro Optimizations

At this point we've tackled the obvious wins. There were still a couple smaller areas for improvement though. For example, our private next() function was serving two purposes:

1. Consume the next character regardless of what it is
2. Consume the next character only if matches the input; throw an exception otherwise

Even though the if() check was already extremely fast, it's still faster to not perform it in the first place. I therefore split this into two separate functions and ensured the code used the most-appropriate one:

     /**
      * Parse the next character.
      *
-     * If $c is given, the next char will only be parsed if the current
-     * one matches $c.
-     *
-     * @param string|null $c
-     *
      * @return null|string
      */
-    private function next($c = null)
+    private function next()
     {
-        // If a c parameter is provided, verify that it matches the current character.
-        if ($c !== null && $c !== $this->ch) {
-            $this->throwSyntaxError(sprintf(
-                'Expected %s instead of %s',
-                self::renderChar($c),
-                self::renderChar($this->ch)
-            ));
-        }
-
         // Get the next character. When there are no more characters,
         // return the empty string.
         if ($this->ch === "\n" || ($this->ch === "\r" && $this->peek() !== "\n")) {
             $this->at++;
             $this->lineNumber++;
             $this->columnNumber = 1;
         } else {
             $this->at++;
             $this->columnNumber++;
         }
 
         $this->ch = $this->charAt($this->at);
 
         return $this->ch;
     }
 
+    /**
+     * Parse the next character if it matches $c or fail.
+     *
+     * @param string $c
+     *
+     * @return string|null
+     */
+    private function nextOrFail($c)
+    {
+        if ($c !== $this->ch) {
+            $this->throwSyntaxError(sprintf(
+                'Expected %s instead of %s',
+                self::renderChar($c),
+                self::renderChar($this->ch)
+            ));
+        }
+
+        return $this->next();
+    }
+

I also found another frequently-used check to see whether the current position was negative - this was pointless because that value is always 0 or higher, so it was removed:

     private function charAt($at)
     {
-        if ($at < 0 || $at >= $this->length) {
+        if ($at >= $this->length) {
             return null;
         }
 
         return $this->chArr[$at];
     }

As expected this didn't provide a major improvement, but every millisecond counts!

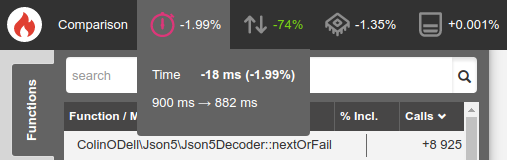
Handling Standard JSON

At this point I felt the improvements were good enough to release, but then Antonio added a new comment:

Taking in consideration json_decode() is able to decode a 65000 lines JSON in 17ms, it may be worth doing two calls (every single time) for those who, like me, tried to completely drop json_decode() and just use json5_decode().

In other words, why not try parsing the input as normal JSON first and only "fall-back" to JSON5 when needed? This was a brilliant idea!

• Best case: We have vanilla JSON and can immediately return a result from PHP's super-fast implementation
• Worst case: We've only wasted a few milliseconds, even for massive inputs

There was a catch though: prior to PHP 7, json_decode() had some non-standard behaviors and edge cases which aren't compatible with JSON5 and other JSON implementations. This meant we could only apply this optimization for users on PHP 7:

public static function decode($source, $associative = false, $depth = 512, $options = 0)
{
    // Try parsing with json_decode first, since that's much faster
    // We only attempt this on PHP 7+ because 5.x doesn't parse some edge cases correctly
    if (PHP_VERSION_ID >= 70000) {
        $result = json_decode($source, $associative, $depth, $options);
        if (json_last_error() === JSON_ERROR_NONE) {
            return $result;
        }
    }

    // Regular JSON parsing failed; fallback to our JSON5 parsing

    // ...
}

As a result, anyone on PHP 7 should not see any performance penalty when using this JSON5 library to parse standard JSON!

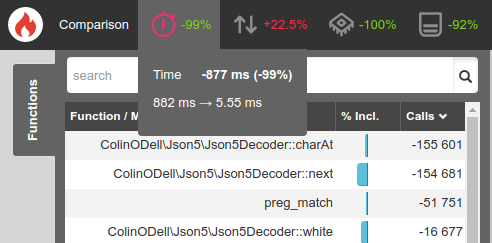
PHP 5 can't take advantage of this, but it still benefits from all the other optimizations we made.

Summary

As a result of these improvements, parsing JSON5 is now 98% faster! Massive documents that previously took minutes can now be parsed in under a second!

It's even faster if you're parsing standard JSON on PHP 7 with this library - that's more than 99% faster!

I am extremely pleased with these results and very thankful to the folks behind Blackfire for creating such a great tool for performance profiling!

UPDATE

After sharing this article on Reddit, Nikita Popov pointed out that my usage of mbstring was probably unnecessary:

I took a closer look and realized he was mostly right - every bit of syntax I care about uses a single byte and the parser will always stop or advance by single-byte chars. I really only needed to handle multi-byte characters in two instances:

1. Checking for UTF-8 encoded non-breaking spaces
2. Determining the character column position in the current line when throwing helpful syntax errors.

I therefore switched everything to use byte offsets, handled #1 by simply checking the current and next byte, and handled #2 by only calculating the column position using mbstring functions if/when such error needs to be thrown.

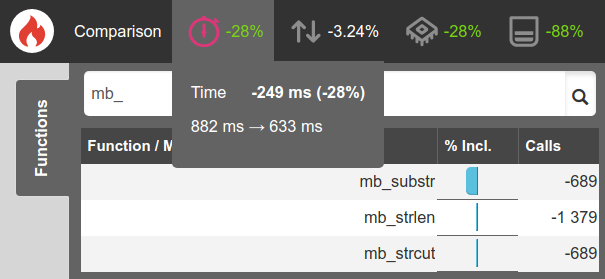
This let me squeeze out another 28% boost in CPU time and an 88% reduction in memory!